Mahoor Mehdikhani (KU Leuven)

Latest publications by this author

Translaminar fracture in (non–)hybrid thin-ply fibre-reinforced composites: An in-depth examination through a novel mini-compact tension specimen compatible with microscale 4D computed tomography
Sina AhmadvashAghbash, Guillaume Broggi, Abdullah Aydemir, Alexios Argyropoulos, Joël Cugnoni, Véronique Michaud, Mahoor Mehdikhani, Yentl Swolfs
Translaminar fracture toughness is pivotal for notch sensitivity and damage tolerance of fibre-reinforced composites. Hybridisation offers a promising pathway for enhancing this parameter in thin-ply composites. Three novel mini-compact tension specimen geometries were investigated for their competence in microscale characterisation of translaminar fracture using in-situ synchrotron radiation computed tomography (SRCT). Only “mini-protruded” design resulted in stable crack propagation with adequate crack increments. Based on this design, five baseline and hybrid cross-ply configurations incorporating low- and high-strain carbon fibres were studied. Crack propagation in low- and high-strain baseline configurations was stable. For interlayer and intrayarn fibre-hybrid configurations, a correlation between load–displacement curves and delamination is observed. The SRCT data confirmed that 90° ply-blocks cushion the interaction between 0° plies, enabling independent fracture. Additionally, crack fronts in 90° plies advance further than those in 0° plies. Moreover, mechanical interlocking and bundle bending within 0° plies serve as supplementary mechanisms for energy dissipation.
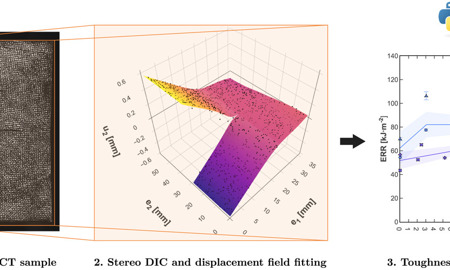
Implementation and parametric study of J-integral data reduction methods for the translaminar toughness of hierarchical thin-ply composites [OPEN ACCESS]
Guillaume Broggi, Joël Cugnoni, Véronique Michaud
Three different J-integral formulations to derive the experimental translaminar toughness of composites from compact tension tests with a large-scale fracture process zone are implemented and discussed. They improve the existing approaches by taking advantage of stereo-digital image correlation to acquire full-field displacement fields. A field fitting procedure based on robust and efficient piecewise cubic smooth splines addresses noise-related issues reported in previous studies. Additionally, the paper proposes a novel crack tip extraction procedure to report the energy release rate as a function of the crack increment, even if knowledge of the crack tip is not required for the proposed J-integral method. The three methods are discussed in light of a parametric study conducted on synthetic and experimental data, including artificially noisy data. The study reveals that the proposed J-integral methods are suitable for translaminar toughness evaluation of a wide range of materials without the need for restrictive assumptions. However, variations in propagation values were observed when applied to experimental data. Finally, guidelines are drawn to chose the most suitable parameters for the algorithms that are proposed as a Python package.
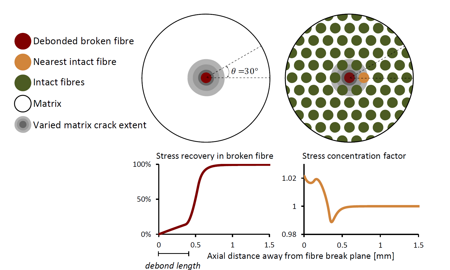
Longitudinal debonding in unidirectional fibre-reinforced composites: Numerical analysis of the effect of interfacial properties
Sina AhmadvashAghbash, Christian Breite, Mahoor Mehdikhani, and Yentl Swolfs
Longitudinal fibre-matrix debonding is governed by interfacial strength, fracture toughness, thermal residual stresses, friction, and matrix plasticity. The proposed finite element model for fibre-matrix longitudinal debonding associated with fibre breakage accounts for these features, retrieving more realistic results for the stress redistribution around a fibre break. In contrast with the majority of the available finite element models, the current model does not impose the debond length and enables debond propagation based on the assigned interfacial properties. Several parametric studies have been performed to assess the effect of input parameters in two configurations: single- and multi-fibre packings. Higher values for interfacial friction coefficient, thermal residual stress and interfacial fracture toughness restrain the debond propagation and consequently accelerate the stress recovery. Conversely, including matrix plasticity facilitates the debond propagation. A prescribed matrix crack, concentric with the broken fibre and as large as thrice the fibre radius, has no significant effect on the extent of the debond but increases the stress concentration on the nearest intact fibres in the multi-fibre model. The results of the proposed finite element model match the reported laser Raman spectroscopy literature data. The current study improves the prediction capability of models for the longitudinal tensile failure of unidirectional composites.

